低コスト・低消費電力ソリューションのためのアーキテクチャ最適化手法

　はじめに

　低コスト・低消費電力デバイスの競争が激化する中、半導体ベンダと顧客企業は、より微細化した先端プロセスノードの開発と活用に邁進しています。IBSによると、新チップの開発にかかる総コストは、65nmプロセスノードの平均4500万ドルから、22nmプロセスノードでは平均1億5000万ドルに増大しています。NRE投資額の高騰はあるにしても、結果的にはチップコストと電力消費の低減で見合うものになるとされています。

　デバイスのコストや消費電力を低減する直接的な方法として他に考えられるのは、アーキテクチャとサイズの最適化です。この最適化手法は比較的コストがかからずにすむのですが、案外見落とされがちで、コストと消費電力削減の機会を逃しています。本レポートでは、先進プロセスノードに投資してコストと消費電力の削減を目指すよりも、時には何倍も効果が期待できるアーキテクチャ最適化の例を紹介します。当然ながら、先進のプロセスノードとアーキテクチャ最適化を組み合わせれば、コストと消費電力の削減が最大化できます。

　ここで紹介するアーキテクチャ最適化手法(デジタルフィルタを用いる演算・信号処理に係わる最適化)は次の通りです。

特定の性質を持つアルゴリズムを活用したサイズ縮小(例:シンメトリ/対称性)代数的性質を利用したサイズ最適化(例:複素乗算)データスループットのボトルネック解消(例:ダブルデータ/処理、レート変換インタフェース)アーキテクチャ最適化 – コストと消費電力の削減可能性

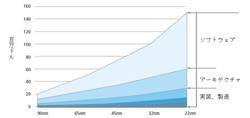
　図1は、プロセスノードの進展に伴う、チップ開発コストの急激な増大の度合いを示しています。

　図1 プロセスノードとチップ開発コストの関係

　半導体ベンダが先進のプロセスノード開発への投資額をあえて増やす主な理由は、コストと電力消費の削減が確実に期待できるからです。

　図2に示す通り、プロセスノードが進化し微細化すればするほど、概してデバイスコストは低下します。しかし、プロセス技術が成熟して、前世代のプロセスノードよりも高い歩留まりを得るまでには、ある程度の時間がかかります。図中で、最低コストを示すポイントが、最先端プロセスノードではなく、2世代前のノードにあるのはそのためです。Fpはプロセスコスト最適化係数です。この例では、Fpは65nmで製造されたシリコンデバイス(ポイントA)と、45nmで製造されたシリコンデバイス(ポイントB)との間のアーキテクチャ最適化なしでのコスト比です。Faはアーキテクチャによるコスト最適化係数です。この例では、Faは45nmで製造されたシリコンデバイスでアーキテクチャ最適化なし(ポイントB)と、アーキテクチャを最適化あり(ポイントD)との間のプロセスコスト最適化係数です。すなわちコストの最適化は、65nmプロセスから45nmに移行し(ポイントAからポイントB)、さらにアーキテクチャの最適化を行うことの組み合わせで(ポイントD)達成できるのです。

　注:図2と図3はデバイスコストと消費電力の傾向を定性的に示したものであり、プロセスノード間の正確かつ定量的なコストを示すものではありません。実際の数値は、パラメータごとに異なり、その点については本レポートでは取り上げません。

　図2 デバイスコストの最適化

　図3は、図2と同じプロセスノードにおけるデバイス消費電力の最適化をグラフに表したものです。最低電力消費量は、プロセスを32nmから22nmに移行して(Fp、ポイントAからポイントB)、さらに22nmプロセスでアーキテクチャ最適化を行うことで(Fa、ポイントBからポイントD)達成されます。

　図3 デバイスの消費電力の最適化

(演算アルゴリズムを考慮した)アーキテクチャ最適化 – シンメトリ

　無線通信や映像アプリケーションにおける信号処理アルゴリズムの多くは、その特性を活用してアーキテクチャを最適化することが可能です。無線通信や映像・音声機器では、FIRフィルタベースのアルゴリズム実装や応用が非常に一般的であり、そのフィルタ係数は図4で示すような、シンメトリ(左右対称)構造になっています。偶対称のFIRフィルタでは、タップ数が偶数で、かつ中央から同じ距離にある2つの係数値が同じで、これは全てのタップに当てはまります。したがって、同一係数値に位置する2つのデータサンプルの加算を先に行うことで、乗算を一度に減らすことが可能です。これに伴い、FIRフィルタの実装に必要な乗算器や付随するロジック(パラレル実装のための加算器、累算器、パイプラインレジスタ、およびメモリ)が半分ですみます。奇対称FIRフィルタの場合は、タップ数が奇数で、偶対称と同様にそれぞれ中央から同じ距離にある2つのタップが同じ値の係数を持ちますが、偶対称と異なり中央の係数のみは同じ係数値を持つタップがありせん。したがって、奇対称FIRフィルタの実装に必要な乗算器の数は、(n-1)/2個減らすことができます(nはタップ数)。この値は、奇対称FIRフィルタのタップ数が増えるにつれて、1/2に近づきます。

　 この場合のデジタルフィルタでは、あるサンプル時刻での出力応答を得るために、理論的にタップ数Nと同じ回数の乗算が必要。従って、何も考慮せずに、素直にサンプルごとに全並列処理で回路実装する場合、N個の乗算器が必要となる。

　図4 奇対称FIRフィルタ

偶対称性の定義

　Y(i)=h(1)×X(i+n)+h(2)×X(i+n-1)+…+h(n-1)×X(i+2)+h(n)×X(i+1)

　係数:h(1)=h(n), h(2)=h(n-1),…{nは偶数}

　したがって

　Y(i) = h(1)×[X(i+n)+X(i+1)]+h(2)×[X(i+n-1)+X(i+2)]+…+h(n)×[X(i+n/2)+X(i+n/2+1)]

奇対称性の定義

　Y(i)=h(1)×X(i+n)+h(2)×X(i+n-1)+…+h(n-1)×X(i+2) +h(n)×X(i+1)

　係数:h(1)=h(n), h(2)=h(n-1),…{nは奇数}

　したがって

　Y(i)=h(1)×[X(i+n)+X(i+1)]+h(2)×[X(i+n-1)+X(i+2)]+…+h(n-1)×[X(i+(n+1)/2+1)+X(i+(n+1)/2-1)]+h(n)×X(i+(n+1)/2)]

　一部のアプリケーションでは、さらに活用可能な特性をもつ対称係数FIRフィルタがあります。これはハーフバンド対称係数フィルタと言われ、図5に示すように中央タップを除き、係数値が1つおきにゼロになります。こうしたフィルタは対称性を持つな奇数タップFIRフィルタでもあるため、必要な乗算器の数を最大約4分の1に減らすことができます。

　図5 対称性をもつハーフバンドFIRフィルタ

映像機器アプリケーションでの2次元シンメトリ

　映像機器アプリケーションにおいて、2次元(2D)係数対称フィルタでの演算は非常に一般的です。図6に示す例のような5×5の2D FIRフィルタは水平・垂直両方向で係数値が対称になっており、同じ色の円が同じ係数値を示しています。こうした映像機器の典型的な2D対称性を活用し、同じ係数値の位置にある全てのピクセルデータに対して単一の乗算器を用いることができます。図6に示す例では、同じ係数値となるピクセルデータ数は4/2/1の3通りがあります。したがって、このような一般的なマトリックスでの乗算器数の削減は最大4分の1までとなります。

　図6 映像機器アプリケーションの2次元対称係数フィルタ例

代数的手法によるアーキテクチャ最適化 – 複素乗算

　無線および有線通信アプリケーションの多くは、複素ドメイン(直交シンボル変調など)実装されるアルゴリズムに基づいています。

　複素サンプル(a+jb)と複素係数(C+jD)間の複素乗算は、4つの乗算で実装できます。

　(a+jb)×(C+jD)=(a×C-b×D)+j(a×D+b×C) {4つの乗算}

　しかし多少の代数的操作により、次のように3つの乗算で同じ解が導けます。

　=a×C-b×D+(a×D-a×D)+j(a×D+b×C+(a×C-a×C))

　=a×(C+D)-(a+b)×D+j(a×(C+D)+(b-a)×C) {3つの異なる乗算}

　乗算器を実装するために必要なシリコンエリアは、加減算器のエリアよりも大幅に大きいため、この3つの乗算の実装により、サイズが約4分の3に減ることになります。

スループットの観点からのアーキテクチャ最適化 – ダブルデータ(処理)レート

　ダブルデータレートによるスループットの最適化は、FPGAデバイスにありがちなファブリック・スループットの問題を克服するために考案された特別なアーキテクチャ手法です。FPGAのDSPスライスは、類似するプロセスノードのASICとほぼ同じサイズ効率を持ちますが、機能的な柔軟性はASICよりも優れています。問題は、FPGAの使用率が高い多くの実際的事例において、ファブリックの比較的低い動作周波数が、高効率DSPスライスにスループットのボトルネックを生じさせる点です。この問題に対応するために、LatticeECP4はスループットを向上させる革新的なインタフェースをDSPスライスに組み込むことによって、他のFPGAデバイスと比較して2倍のスループットを達成しています。この性能向上機能(図7)により、LatticeECP4デバイスは、必要とする乗算器の数を通常の半分に減らしながら、同じように複雑なDSP機能を実装できます。こうした最適化により、より小規模のデバイス(必要に応じて、より小さなフォームファクタを持つデバイス)に機能を実装することができ、システムコストとサイズ、および消費電力を削減できます。

　図7 FPGA DSPスライスのスループットの最適化

　多くの場合、異なるアーキテクチャ最適化手法を組み合わせて、より高いレベルのコスト削減や省電力化を達成することが可能です。図8は、ダブルデータレートと対称性を組み合わせたアーキテクチャ最適化手法を示しています。前述のように無線通信や映像機器アプリケーションに実装されているほとんどのFIRフィルタは係数対称であり、無線通信ではデジタルダウンコンバータ(DDC)やデジタルアップコンバータ(DUC)といった機能が該当します。図8の設計例が示すのは、入力データレート要件が245.76Mspsの、64タップ係数対称FIRフィルタです。ダブルデータレートや対称性に対応したDSPスライスを組み込んでいない一般的なFPGAデバイスの場合、このFIRフィルタに18×18乗算器が64個必要です。LatticeECP4の場合、同じFIRフィルタを16個の18×18乗算器で実装でき、4分の1に削減されます。実質的に用いられるシリコンサイズの縮小により、電力消費量が約半分に低減し、或いはより小規模のFPGAデバイスに実装できることで、コスト削減やより小型化というシステム要件に対応できるようになるなど、様々なメリットを享受できます。

　図8 FPGA DSPスライスのスループットおよび対称性の最適化

　同様にハーフバンドフィルタやダブルデータレートによる最適化も、他のDDCまたはDUC補間フィルタや間引きフィルタに導入できます。この場合コスト削減率はさらに高く、コストは約8分の1に消費電力は4分の1に低減できます。

　図9は、ダブルデータレートによる最適化手法をその他のコスト削減手法と組み合わせた場合の、FIRフィルタタップ数に対する総合的なコスト削減率を表しています。

　図9 ダブルデータレートとその他の最適化手法との組み合わせ

　LatticeECP4 FPGAファミリは、本レポートで記述したすべてのアーキテクチャ最適化手法に対応しており、無線通信や映像機器といった乗算器を多用するアプリケーションのコストと消費電力の削減を達成する上で最適と言えます。

まとめ

　アーキテクチャ最適化は、シリコンデバイスのコストと消費電力を下げるにあたって、比較的安価な方法です。多くの場合、データフロー最適化、アルゴリズムの特性を踏まえた最適化、或いは代数的演算による最適化といった、異なる最適化手法を組み合わせることで、コストや消費電力を半分から8分の1に削減することができます。半導体ベンダーやその顧客企業は、低コストで効果の高いこうした手法を活用することを推奨します。

著者紹介

　Asher Hazanchukproduct planning manager for Lattice Semiconductor, focusing primarily on the Security and Video Surveillance markets