コンピュータアーキテクチャの話 (101) 浮動小数点除算器と平方根演算器

　浮動小数点除算器

　浮動小数点の乗算の場合は、仮数部の掛け算と指数部の足し算を行ったが、浮動小数点の割り算は、仮数部の割り算と指数部の引き算を行えば良い。仮数部の割り算は、このコラムの84回から説明した整数の割り算とほぼ同様であるが、最上位の”1″の位置が揃っているのでゼロスキップの必要が無い点と、整数の割り算の場合は、1の桁までの商を求めれば終わりであるが、浮動小数点の割り算の場合は、小数点以下の商をガードビットやラウンドビットを含めた有効数字の最下位の桁まで求める必要がある点が異なる。しかし、これは割り算のループの終点が異なるだけであり、回路としては整数の場合と同じ構造で計算できる。

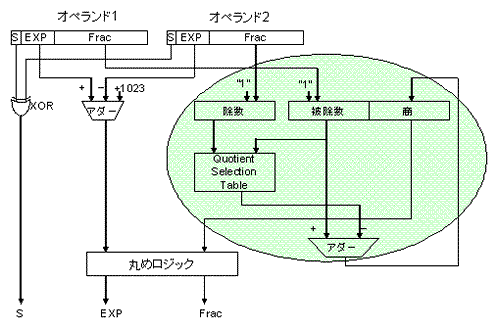
　割り算のオペランドの仮数部は1.0以上、2.0未満の範囲であるので、仮数部の割り算の結果は0.5より大きく、2.0未満となる。このため、仮数部の割り算結果が1.0未満となった場合は、1ビット左シフトを行い、指数部の引き算結果から-1する必要がある。また、指数の計算は、被除数の指数部から除数の指数部を引くと、バイアスが無くなってしまうので、バイアス分を加算する必要がある。ということで、浮動小数点除算器の構成は、次の図23のようになる。

　図23:浮動小数点除算器の構成。緑の楕円で囲んだ部分は繰り返し使用される。

　なお、これまでに説明してきた浮動小数点の加算、乗算、積和演算回路は、入力から出力までをパイプライン構造とすることができ、1サイクル毎に新しいオペランドを入れて演算を開始することができるが、図23の除算器は、一つのオペランドペアに対する割り算に、緑の楕円で囲んだ回路が繰り返し使われるので、一つの計算が終了するまで、次の割り算を開始することはできない。

平方根演算器

　SRT割り算器を、多少改造すると平方根も計算できる。10000(10の4乗)の平方根は100(10の2乗)というように平方根をとると、指数の値は元の数の指数の半分になる。この結果の指数が整数であるためには、元の指数は偶数でなければならない。また、以下で述べるアルゴリズムでは、平方根を求める入力オペランドは1.0未満の数としているので、もとの指数が奇数(IEEE 754では、単精度の場合は127、倍精度の場合は1023とバイアスが奇数であるので、EXP部の値としては偶数)の場合は、仮数部分を1ビット右シフトして、指数を＋1して偶数とする必要がある。また、元の指数が偶数の場合は仮数部分を2ビット右シフトして指数は偶数で、仮数部の値を0.5未満の範囲とする必要がある。結果として、平方根を求める仮数部の値は0.25以上、1.0未満となる。以下の説明ではこのように調整された入力オペランドをAと呼ぶ。

　j桁まで計算した時点でのSQRT(A)の近似値をS(j)、残差 を

　とする。ここでrは計算のRadixである。そして、繰り返しの最初にはAを残差Wとする。つまり、W(0)＝Aである。また、s(0)はゼロである。こう定義すると、S(j)の次の桁としてs j+1を選ぶと、次のj+1桁目の残差は、

　と表わされる。このj+1桁目の残差が一定の範囲内に納まり、jが増加して最終桁のnに達したときに、r^(-n)×W(n)がゼロ(あるいは、W(n)の絶対値がr/2以下となり、有効桁数の範囲では、これ以上小さくなりえないよう)になればS(n)がAの平方根となる。従って、平方根を求める問題は、このようにW(j+1)が一定の範囲内に納まるようなs j+1の値を、どのようにして選ぶかという問題となる。これは整数の割り算のところで説明した、商の次の桁をどう選ぶかという問題と似ている。

　詳細は省略するが、Radixを4として、最小冗長シンボル割り当てで各桁を(-2、-1、0、1、2)の範囲で選ぶ場合には、s j+1としてkを選ぶことができる最大値Ukと、最小値Lkは次のように表わされる。

　そして残差W(j)が、s(j)とjから計算されるこのUk(j)とLk(j)の間にあれば、s j+1としてkを選ぶことができる。

　このコラムの整数のSRT割り算の項で、縦軸を部分剰余P、横軸を除数DとしたP-D Plotを説明したが、この平方根の次の桁の選択は、整数の割り算と同様に、横軸を部分平方根(Root:Rと表わす)、縦軸を残差(Partial Remainder:PR)としたR-PR Plotで表現することができる。

　割り算のP-D Plotでは横軸は除数Dであり、計算の途中で変化せず一定であったが、平方根の場合は、Rの値は繰り返しに従って変化する。また、それよりも問題なのは、Uk、Lkに4^(-(j+1))という項が含まれており、繰り返しに従って、毎回、Uk、Lkが変化してしまう。従って、Uk、Lkがjに依存しない割り算と異なり、厳密には、jの値に応じて次の桁の値を選択するテーブルを切り替える必要がある。

　しかし、j=1とj=28のU0とL1をプロットしてみると、次の図24のようになる。ここで上側の2本の線の下の領域はs j+1として”0″を選んで良い領域であり、下側の2本(殆ど1本のように見える)の線の上側の領域は、s j+1として”1″を選んで良い領域である。つまり、この間の領域は、s j+1として”0″でも”1″でも良いという重なりの領域である。

　図24:U0とL1の最大と最小のプロット

　図24に見られるように、それぞれの最大値と最小値の差はあまり大きくなく、安全サイドでU0の最小値とL1の最大値をとっても、重なりの領域は十分残っている。このように、Uの下限と、Lの上限を使ってR-PR Plotを作ったのが、図25である。

　図25:平方根のR-PRプロット

　この図では、S(j)を0.125刻み、4*W(j)を0.25刻みで目盛り線を書いているが、一つのマスに”0″と”1″、あるいは”1″と”2″のように異なる値が入っていることはなく、”0 or 1″あるいは、”1 or 2″とくっつければ、マスごとに選択するs j+1の値を一意に決めることができる。つまり、s(j)を4分割し、W(j)側は、U2のmaxを考えると0.5刻みで、5.5までの22分割のテーブルを作れば、平方根の計算ができる。

　図26:平方根計算回路の構成

　平方根を計算する回路の構成は図26のようになる。Adjustと書いた箱は、入力オペランドの仮数部を1.0未満、指数部を偶数に変換する回路である。そして、0.25以上、1.0未満に変換されたオペランドを部分残差Wの初期値として出力する。

　平方根計算回路の心臓部は、その時点での平方根のs(j)と部分残差W(j)の上位ビットからs j+1を予測するテーブルと、s j+1の1、2、3に対して

　を計算するMultiple Generatorである。これらの部分と平方根レジスタを除くと、部分残差とCSA、CPAは除算回路と同じであり、一般的には、これらの部分を共用して、除算と平方根の両方が計算できるユニットとして実装される。

　そして、指数部は、Adjustの結果の指数を1/2にして、更に、丸めの影響を補正して出力のEXP部が作られる。なお、IEEE 754の体系では虚数は扱えないので、符号部Sが”1″になった負の数が入力された場合は非数(NaN)を出力する必要があるが、図26の回路では、このような異常処理については省略している。

　Multiple Generatorであるが、s j+1は-2～+2の範囲の数であるので、最初の項はs(j)を左シフトし、必要に応じて2の補数化してやれば生成でき、第二項もs j+1の2乗は0、1、4であり、それをjの値に応じて右シフトすれば良いので、比較的容易に生成できる。