コンピュータアーキテクチャの話 (80) Boothのアルゴリズム

　

　パラレルアダー方式の乗算器は64ビットの乗算でも、アダー6段程度の遅延、あるいは6クロック程度で乗算が実行出来るという点で高性能であるが、部分積の数-1個の大量のアダーを必要とし、膨大な物量を必要とするのが欠点である。しかし、部分積の数を減らすことが出来れば、必要なアダーの個数を減らすことが可能となる。

　これまで述べてきた方法は、乗数1ビットに対して一つの部分積を作ってきたが、複数の乗数のビットをまとめて処理すれば部分積の数を減らすことが出来る。例えば、乗数を2ビットづつまとめて取り扱うと、"00"の場合は加算無し、"01"の場合は被乗数を加算し、"10"の場合は被乗数の2倍、"11"の場合は被乗数の3倍を加算すれば良い。しかし、ここで問題になるのが、被乗数の3倍をどうやって作るかという点である。被乗数の2倍は、単に1ビットの左シフトで良いが、3倍を作るには加算回路が必要になってしまう。

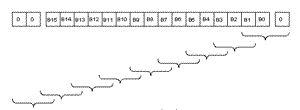
　これを回避する方法として考案されたのが、ブース(Booth)のアルゴリズムと呼ばれる方法である。ブースのアルゴリズムでは、乗数を2ビットごとに処理する場合は、下図のように乗数の最下位B0の下に1ビットの"0"、最上位(ここではB15)の上に2ビットの"0"を補い、ブラケットで囲んだ3ビットごとに処理する。

　Radix-4のBoothアルゴリズム。3ビットの乗数のグループごとに加算する値を選択

　そして、被乗数をMとすると、下記の表のように加算値を選択する。

　 3ビットの乗数 加算値

000+0 001+M 010+M 011+2M 100-2M 101-M 110-M 111+0

　

　最初は、最下位は追加された"0"であるので、B1、B0の2ビットが"00"の場合は+0、"01"の場合は+M、"10"の場合は-2M、"11"の場合は、-Mが加算される。しかし、次回の計算ではB3、B2、B1の3ビットを検査するので、B1のビットは次回の加算値の選択にも影響する。B3、B2が"00"である場合は、B1が"1"であると上の表から＋Mであるが、2ビットシフトされていることを考慮すると+4Mが加算されることになる。つまり、B1、B0が"10"の場合は-2M+4Mで、結果として+2Mが加算され、B1、B0が"11"の場合は-1M +4Mで、結果として+3Mが加算されることになる。B3、B2が"01"の場合は+8M、"10"の場合は-4M(B3が次の回で+16Mになるので、結果として+12M)、"11"の場合は+0(B3が次の回で+16Mになるので、結果として+16M)となり、 B3、B2が"00"の場合と同様に、B1 が"1"であると+4M大きい値が加算され、前回の加算値と合わせると正しい値になるように工夫されている。

　このようにブースのアルゴリズムを用いることにより、M、2Mという1ビットずらせて配線することだけで作れる値を加減算するだけで、乗数を2ビット単位で処理して部分積の数をN/2+1とほぼ半減することができる。

　このブースのアルゴリズムを用いて2ビット単位で乗数を処理する乗算器の回路を次の図に示す。

　2ビット単位で処理するブースのアルゴリズムを用いた乗算器

　3ビットの乗数の組み合わせから0/M/2Mを選択する信号と+/－を指定する信号を作るブースエンコーダが追加され、アダーの入力のマルチプレクサの入力に2Mの入力が追加されているが、1ビット単位で処理する乗算器と比べて大差ない物量であり、これで加算の回数がN-1回からN/2回に減少するのは大きなメリットである。

　まとめて取り扱う乗数のビット数を2ビットづつではなく3ビットづつ処理するようにブースのアルゴリズムを拡張することも可能であるが、この場合は3Mを作る必要が出てくる。これを実現するためには、下図のように3Mを保持するレジスタを追加し、最初にMPX1とMPX2でMと2Mを選択して加算し、3Mを計算してレジスタに格納するようにすれば良い。

　乗数を3ビットごとに処理する乗算器の構成

　そして、乗数を4ビットのグループで1ビットづつオーバラップさせて処理し、MPX1とその下のXORで+M、+2M、+3M、+4M、-4M、-3M、-2M、-Mを選択して加算する。このように3ビットづつ処理するためには、若干の追加のハードウェアと最初の3Mを計算するステップが必要となるが、繰り返しの回数がN/3+1回に減少するので、Nが大きい場合には、前述の2ビット単位の処理よりも高速に乗算を行うことが出来る。

　このようにBoothのアルゴリズムを使うことにより、比較的少ない回路の追加で大幅に乗算性能を改善できるので、現在のマイクロプロセサの乗算器では、殆ど例外なくBooth乗算器が使われている。現在のマイクロプロセサでは2ビットづつのBooth処理を行うものが多いが、IBMのメインフレームでは3Mを計算する専用のアダーを設け、乗数を3ビットづつ処理するBooth方式が用いられている。